台集合のサイズがmである単体的複体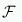 において、サイズがiの要素の個数をFiとすると、
において、サイズがiの要素の個数をFiとすると、
Fi-1 ≧ (i/(m−i+1))・Fi
が成り立つ。
|
スペルナーの定理
台集合のサイズがmである単体的複体 Fi-1 ≧ (i/(m−i+1))・Fi が成り立つ。 |
この定理の証明は簡単である。
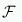 に含まれる集合の部分集合はすべて
に含まれる集合の部分集合はすべて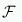 に含まれることから、
に含まれることから、
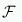 に含まれるサイズiの要素1つに対して、その部分集合としてi個、サイズi−1の要素が存在
している。
に含まれるサイズiの要素1つに対して、その部分集合としてi個、サイズi−1の要素が存在
している。
ここで、包含関係のあるようなサイズiの集合とサイズi−1の集合の組の個数をxとすると、
i・Fi≦(m−i+1)Fi-1
すなわち、Fi-1 ≧ (i/(m−i+i))・Fiという不等式が得られることになる。
(証明終り)
注: このように、ある性質を満たす集合族(この場合は単体的複体である、つまり、部分集合に閉じている集合族)に対して、限界ぎりぎりの状況ではどのようなことが起こっているか?(この場合は、Fi-1をどこまで下げられるか?)というような議論は、「極値集合論」(extremal set theory)と呼ばれる分野で行なわれている。離散数学・組合せ論の重要な分野の一つである。