Poincaré sphere

Description

A manifold which is not homeomorphic to a sphere but has the same homology group as a sphere. This is derived by suitable identifications of facets of a regular dodecahedron.
(Identify the vertices with the same label in the figure below.) The data given here is a triangulation made by Björner and Lutz. This is the smallest triangulation currently known. (16 vertices and 90 facets)

Some property

This is Cohen-Macaulay, but not constructible nor shellable.

Datum

poincare.dat

Some table

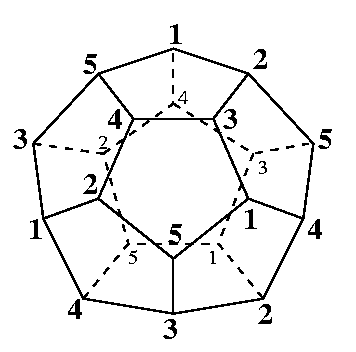
vertex decomposable?	no
extendably shellable?	no
shellable?	no
constructible?	no
Cohen-Macaulay?	yes
partitionable	yes
topology	Homology sphere
f-vector	(1,16,106,180,90)
h-vector	(1,12,64,12,1)
made by	Poincaré, triangulated by Björner&Lutz

References

A.Bjorner and F.H.Lutz, Simplicial manifolds, bistellar flips and a 16-vertex triangulation of the Poincaré homology 3-sphere", to appear in Experimental Mathematics.

F.H.Lutz, Triangulated manifolds with few vertices and vertex-transitive group actions, Shaker Verlag (1999).